Category: Հանրահաշիվ 9

1)Գտե՛ք ֆունկցիայի զրոները.
ա) y = |x|

x=0
բ) y = |x + 2| — 8

x=6, x=-10
գ) y = — 2|x| — 4

Լուծում չունի
դ) y = 3|x — 1| — 6

x=3, x=-1
ե) y = 0.5|x + 2| — 3

x=4, x=-8
զ) y = — 5|x| + 10

x=2, x=-2

2)Գծե՛ք ֆունկցիայի գրաֆիկը.
ա) y = |x + 1|

բ) y = |x — 5|

գ) y = |x + 6|

դ) y = |x — 3|

3)Գծե՛ք ֆունկցիայի գրաֆիկը.
ա) y = |x| + 1

բ) y = |x| + 4

գ) y = |x| — 3

դ) y= |x| — 1

4)Գծե՛ք ֆունկցիայի գրաֆիկը.
ա) y = |x — 1| + 1

բ) y = |x + 4| — 2

գ) y = |x — 3| — 3

դ) y = |x + 6| — 1

1)Տրված է f(x) = |x — 1| ֆունկցիան: Գտե՛ք ֆունկցիայի արժեքը ա) 2, բ) 0, գ) –2 կետում:

1,   1,   3

2)Տրված է f(x) = 2|x + 3| ֆունկցիան: Գտե՛ք ֆունկցիայի արժեքը ա) – 5, բ) 1, գ) –3 կետում:

4, 8, 0

3)Տրված է f(x) = |x — 4| ֆունկցիան: Ո՞ր կետերում է ֆունկցիան ընդունում ա) 2, բ) 0, գ) -4, դ) 7 արժեքը:

6, 4, լուծում չունի, {11, -3}

4)Տրված է f(x) = |x + 9| ֆունկցիան: Ո՞ր կետերում է ֆունկցիան ընդունում ա) 1, բ) 8, գ) -1, դ) 5 արժեքը:

{-10, -8},  {-17, -1},  լուծում չունի, {-14, -4}

5)Նկարում պատկերված է y = f(x) ֆունկցիայի գրաֆիկը: Գծե՛ք y = |f(x)| ֆունկցիայի գրաֆիկը.

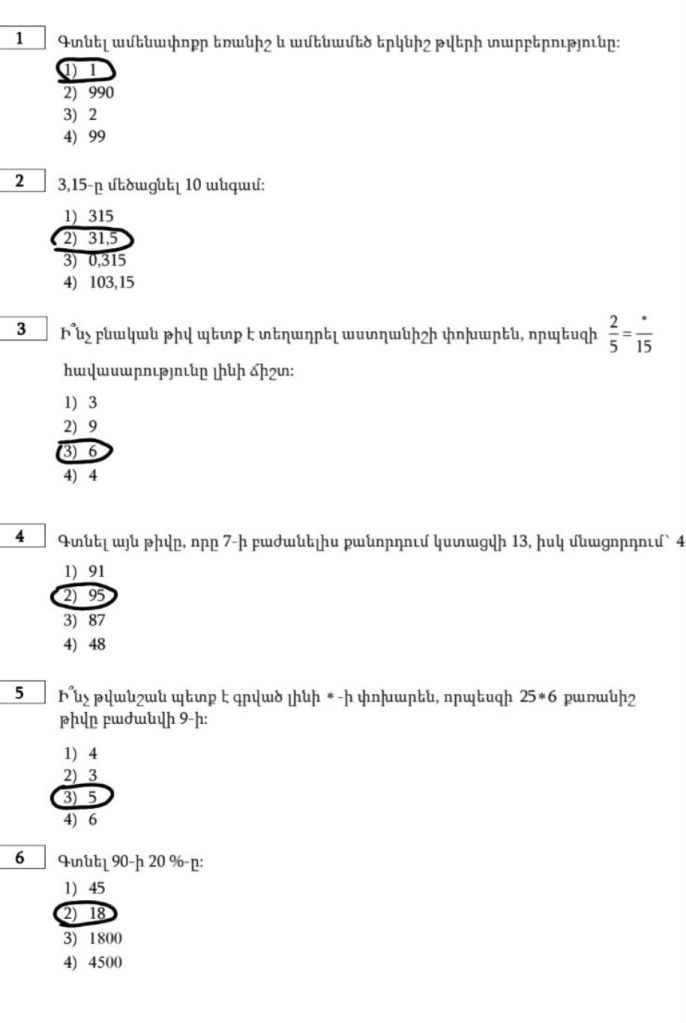
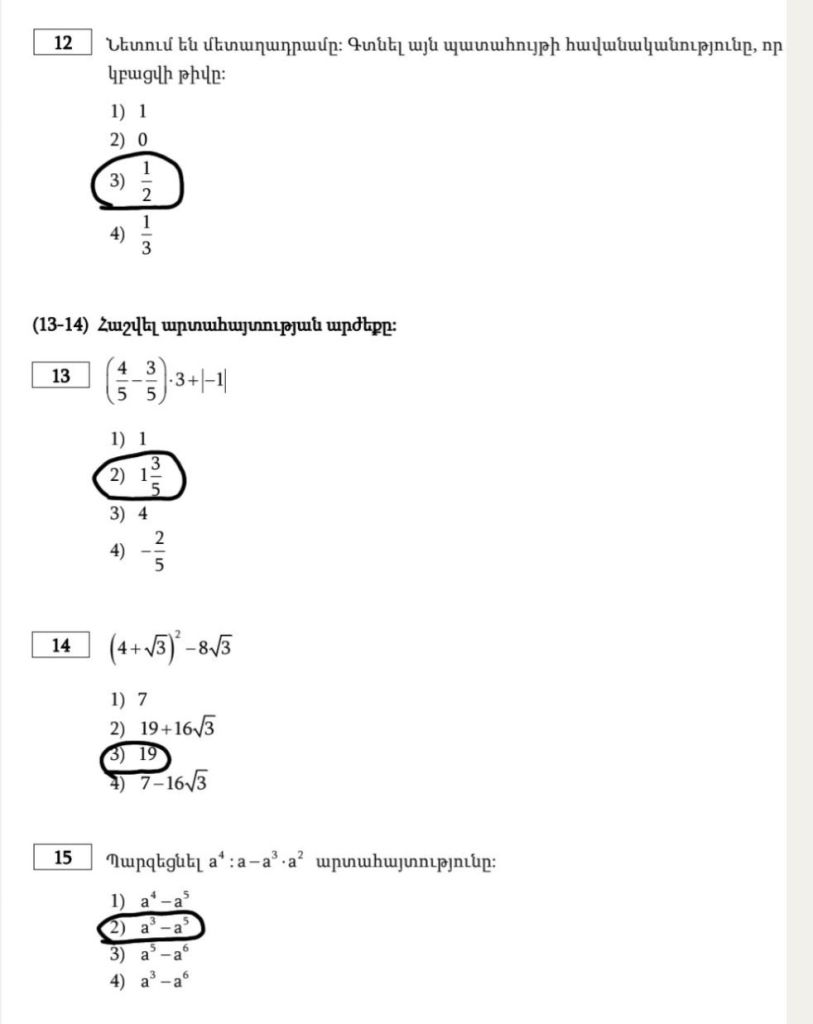
1)Գտե՛ք թվային տվյալների լայնքը, մոդն (եթե ունի) ու մեդիանը.
ա) 2, 2, 2, 5, 5, 8, 10

8, 2, 5
բ) -5, 4, 2, 6, 6, 8, 8, 8

13, 8, 6
գ)-105, 12, 12, 250, 233, 205, 12

-105, 12, 12, 12, 205, 233, 250

355, 12, 12
դ) -20, -120, 0, 15, 7, 7, 120, 500

-120, -20, 0, 7, 7, 15, 120, 500

620, 7, 7

2)Հաշվե՛ք թվային տվյալների միջին թվաբանականն ու մեդիանը.
ա) 1, 3, 3, 5, 7

3,8, 3
բ) 5, 2, 1, -2, 7, -4

-4, -2, 1, 2, 5, 7

1,5, 1,5
գ) 4,5,7,5,-8, 45

-8, 5, 5, 5, 7, 45

9,(6), 5
դ) 2, 2, 8, 8, 8, 250, -120

-120, 2, 2, 8, 8, 8, 250

22,5, 8
ե) 1, 1, 1, 1, 5, 5, -6, -10

-10, -6, 1, 1, 1, 1, 5, 5

-0,25, 1

3)Գտե՛ք թվային տվյալների միջինը, մոդը, մեդիանը և լայնքը.
ա) 0, 0, 5, 5, 10, 10, 10, 10, 10

6,(6), 10, 10, 10
բ) 1, 1, 2, 2, 2, 19, 20, 21

8,5, 2, 2, 20
գ)-6, 6, 0, -3, 3

-6, -3, 0, 3, 6

0, մոդ չունի, 0, 12
դ) –10, 0, 0, 12, 13, 12, 12

5,5, 12, 12, 23

4)Գտե՛ք a-ի թվային արժեքը, եթե հայտնի է, որ a, 1, 1, 2, 2, 4 բնական թվերի՝
ա) մոդը 2 է

2
բ) մեդիանը 1.5 է

1
գ) լայնքը 4 է

0
դ) միջինը 3 է

8
ե) մեդիանը մեծ է մոդից

1

1)Տրված է {a_n} երկրաչափական պրոգրեսիան։ Հաշվե՛ք.

ա)S₇ -ը, եթե a₁ = 1, q = 2

127

բ)S₈ -ը, եթե a₁ = -1, q = 3

-3280

գ)S₄ -ը, եթե a₁ = 8, q = 1/2

15

դ)S₆ -ը, եթե a₁ = 4, q = -3

-728

2)Տրված է {a_n} երկրաչափական պրոգրեսիան։ Հաշվե՛ք S₅ -ը.

ա) a₂ = 4, q = 3

484\3
բ) a₃ = 9, a₄ = 27

121

գ) a₂ = 8, q = -1/2

-11

3)Տրված է {a_n} երկրաչափական պրոգրեսիան։ Գտե՛ք a₁ — ը, եթե

ա)S₄ = 30, q = 2

2

բ)S₆ = -2184, q = 3

-6

գ)S₇ = 5, q = -1

5

դ)S₃ = 91, q = -4

7

4)Տրված է b_n = 3 * 2^{n — 1} երկրաչափական պրոգրեսիան: Հաշվե՛ք.

ա)b₃ + b₄

36

բ)b₅ + b₆

144

5){a_n} երկրաչափական պրոգրեսիայում a₁ = 6, q = -1: Հաշվե՛ք.

ա)S₂₀₂₅ — ը

6

բ)S₂₀₂₆ — ը

6

1)Տրված է 1, 3, 9, 27, … երկրաչափական պրոգրեսիան։ Գտեք նրա հայտարարը և հինգերորդ, վեցերորդ ու յոթերորդ անդամները:

q=3, 81, 243, 729

2)Հաջորդականությունն արդյոք երկրաչափական պրոգրեսիա՞ է.
ա) 1, 8, 15, 21, 26, …; ոչ
բ) 4, 2, 1, 0,5, 0,25, …; այո
գ) -2, 2, -2, 2, -2, …; այո
դ) 0, 4, 16, 64, 256, …: Ոչ

3)Գտեք a_n երկրաչափական պրոգրեսիայի առաջին չորս անդամները, եթե a₁ = 2, q = 0,25 :

0.5, 0.125, 0,03125

4)Տրված է a_n երկրաչափական պրոգրեսիան։ Հաշվեք.
ա)a₃ — ը, եթե a₁= 0,5, q = — 2;

-2
բ)a₄ — ը, եթե a₁ = -2, q = 3;

-54
գ) a₃ — ը և q — ն, եթե a₁ = 3, a₂ = 4;

q=4/3 a3=16/3
դ) a₃ — ը և q — ն, եթե a₁ = — 4, a₂ = 6

q=3/-2 a3=-9

5)Տրված են երկրաչափական պրոգրեսիայի երեք իրար հաջորդող անդամներ.
ա) 7, x, 63։ Գտեք x — ը, եթե x > 0 :

21
բ) 2, x, 18։ Գտեք x — ը, եթե x < 0 :

-6
գ) 3,2; x; 0,2։ Գտեք x — ը ։

0,8

1)Արտահայտությունն արտահայտե´ք a1-ով ու d-ով.
ա) a5 + a10

a1+4d+a1+9d=2a1+13d
բ) a3 + 2a7

a1+2d+2a1+12d=3a1+14d
գ) a7 + a8 — 2a6

a1+6d+a1+7d-2a1-10a=3d
դ) a15 + a17 — 2a16

a1+14d+a1+16d-2a1-30d=0

2){an} թվաբանական պրոգրեսիայում գտեք
ա) a2 և d-ն, եթե a1 = 5, a3 = 13 ;

a2=9, d=4
բ) a1 և d-ն, եթե a2 = 3 , a10 = 19 ;

a1=1, d=2
գ) a2 և d-ն, եթե a12 = — 2 , a3 = 7 ;

a2=8, d=-1
դ) a101 և d-ն, եթե a12 = 20,5 ; a7 = 10, 5 :

a101=198,5 d=2

3)Տրված է {an} թվաբանական պրոգրեսիան։ Հաշվեք․
ա) S20 — ը, եթե a1 = 1 , a20 = 20 ;

210
բ) S13, եթե a1 = 17, a13 = 13 ;

195
գ) S30, եթե a1 = — 10 a30 = 20 ;

150
դ) S17, եթե a1 = 11, a17 = 19 :

255

1)Գտե՛ք տրված թվաբանական պրոգրեսիայի տարբերությունը.

ա) 9, 11, 13, 2
բ) 1, 0, -1, -1
գ) 3, 7, 11, 4
դ) 4, 1, -2, -3
ե) 1, 1.5, 2, 0,5
զ) 7.5, 6.2, 4.9, -1,3

2)Տրված է {a_n} թվաբանական պրոգրեսիայի անդամներից ինչ-որ մեկը և d տարբերությունը: Գտե՛ք պրոգրեսիայի առաջին չորս անդամները.

ա)a₁ = 2 d = 5

2, 7, 12, 17
բ)a₁ = 9 d = — 3

6, 3, 0
գ)a₂ = — 2 d = 1.5

-3,5, -2, -0,5, 1
դ)a₃ = — 7 d = — 3.5

-14, -10,5, -7, -3,5

3)Տրված է {a_n} թվաբանական պրոգրեսիան։ Հաշվե՛ք.

ա)S₁₂ — ը, եթե a₁ = 5, a₁₂ = 35

240
բ)S₉ — ը, եթե a₁ = 4, a₉ = 28

144
գ)S₁₇ — ը, եթե a₁ = 4, a₁₇ = 45

416,5
դ)S₅ — ը, եթե a₁ = 2, a₅ = -8

-15

4)Տրված է {a_n} թվաբանական պրոգրեսիան։ Հաշվե՛ք.

ա)S₁₀ — ը, եթե a₁ = 3, d = 4

210
բ)S₈ — ը, եթե a₁ = 7, d = 1

84
գ)S₁₃ — ը, եթե a₁ = 4, d = -1

-26
դ)S₅ — ը, եթե a₁ = -4, d = 2

0