1)Տրված x-երի համար գտե՛ք y-ի այնպիսի արժեք, որ (x, y) կետը լինի y = x2 պարաբոլի վրա.
ա) x = 0 y=
բ) x = 3 y=9
գ) x = — 3.2 y=10.24
դ) x = 111 y=12321
ե) x = √5.5 y=5.5
զ) x = — √13 y=13
է) x = 2√3 y=12
ը) x = — 6√1.5 y=54
2)Հայտնի է, որ (x, y) կետը պատկանում է y = x2 պարաբոլին: Գտե՛ք y-ի տրված արժեքի համար x-ի բոլոր հնարավոր արժեքները: Քանի՞ այդպիսի x կա.
ա) y = 0 x=0 արժեք չունի
բ) y = 25 x=+,-5
գ) y = 196 x=+,-14
դ) y = 2.89 x=+,-1.7
ե) y = — 16 լուծում չունի
զ) y = -2 լուծում չունի
է) y = 2 x=+,-v2
ը) y = 45 x=+,-v45
3)Ո՞ր կետերում է տրված ուղիղը հատում y = x2 ֆունկցիայի գրաֆիկը.
ա) y = 0 (0;0)
բ) y = 5(v5;-5)(v5;5)
գ) y = — 1.1 գոյություն չունի:
դ) y = 64=(-8;64) (8;64)
4)Կառուցե՛ք y = x2 ֆունկցիայի գրաֆիկի համաչափը x-երի առանցքի նկատմամբ:
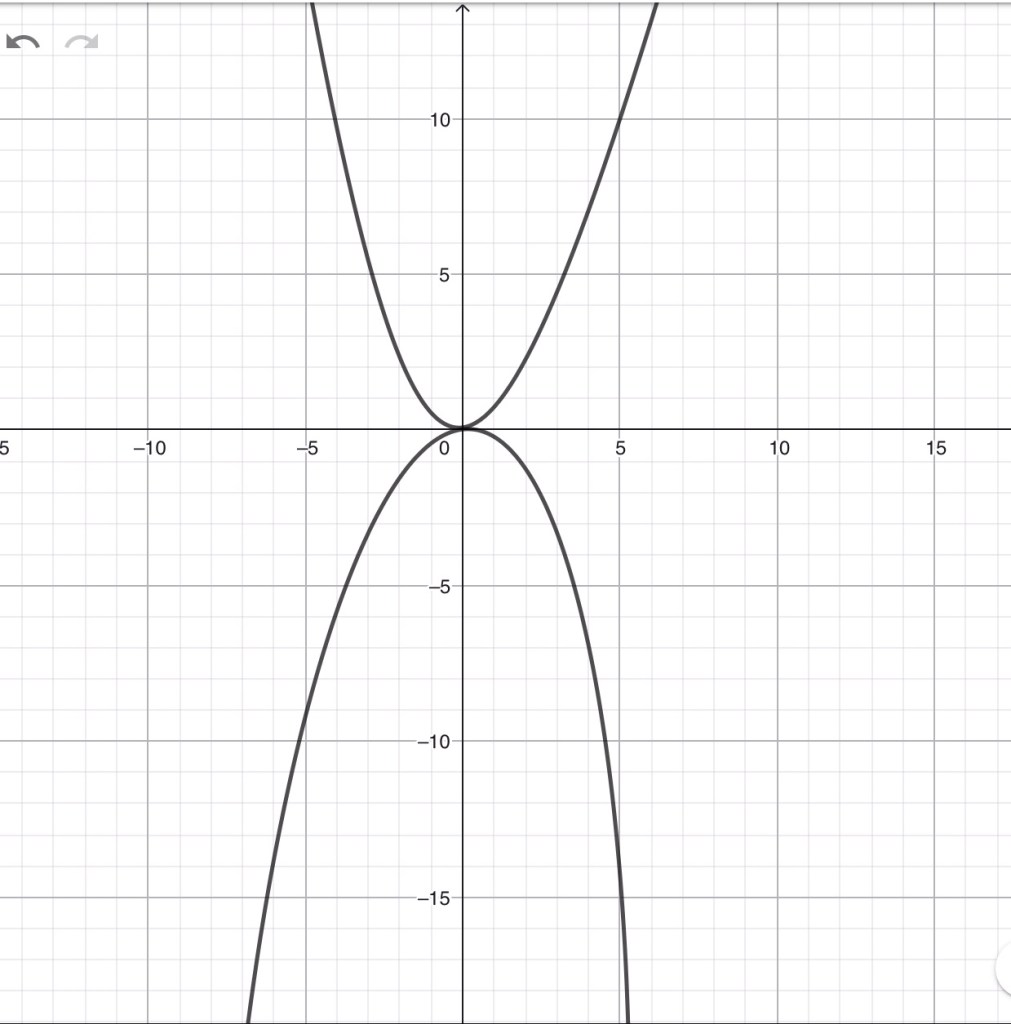
5)Տրված է y = x2 ֆունկցիան: Ո՞ր կետերում է ֆունկցիան ընդունում ա) 9, բ) 0, գ) 15, դ)– 25 արժեքը:
(3;9)
(0;0)
(+,-V15;15)
Դալլաքյան Մարիամ👼 